| Ուղարկել | Բոլոր լուծումները | Լավագույն լուծումները | Վերադառնալ ցուցակին |
ACM_0218 - STAVITEL |
Little Matthew always wanted to be an architect and since his childhood he was spending all his free time building architectonic masterpieces. Due to his limited resources, he built his buildings from wooden unit cubes that he put on top of each other. The columns of the cubes were always placed on a checkerboard with K × K unit squares. Matthew always placed the cubes so that every column covered exactly one checkerboard square.
In the following picture, you can admire one of his creations on a board of size 4 × 4.
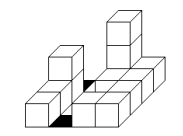
Matthew was proud of his pieces of art. Their order and perfection were unprecedented. How- ever, nobody else shared his enthusiasm. As is usual with most masterpieces, their real value will be understood much later. To preserve his work, Matthew decided to draw the buildings on paper and keep it in a safe place. Because he was unable to draw 3D buildings, he made two 2D drawings: one from the front showing only the front sides of the cubes and one from the right side showing only the right sides of the cubes. In technical terms, his drawings were orthogonal projections.
Have a look at the drawings of the building from the earlier picture:

Matthew believed that these drawings will be enough to reconstruct the buildings later. When he grew up, he realized that he had been wrong. Most of his pairs of drawings could depict many different buildings. After some research, he found out that some buildings may be called minimal because they are composed of the minimum number L of cubes among all buildings whose pair of projections match his drawings. Similarly, he called a building maximal if it used the maximal number M of cubes among all possible buildings.
The following are examples of a minimal and a maximal building for the above pair of drawings. They use L = 7 and M = 17 cubes. They are not as perfect as the original building, but they are still worth your attention.
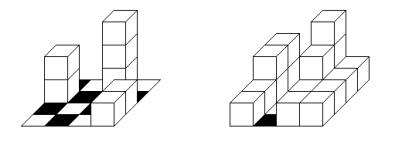
Matthew asked you to write a program that will compute the values L and M for every pair of drawings in his collection.
Input
The first line of the input contains the number of test cases N . Each test case is composed of three lines. The first line of each test case contains a positive integer K ≤ 100, which stands for the width and the height of the square board. The second and the third line describe the drawing from the front and from the right, respectively. Every drawing is described by K space-separated non-negative integers (not higher than 100 000) describing the heights of the K columns of the cubes projection, in the left-to-right and front-to-back order.
You can assume that it is always possible to build at least one building for every given pair of drawings.
Output
For each test case, print exactly one line containing the sentence “Minimalni budova obsahuje L kostek, maximalni M kostek.”, where L and M are the minimal and the maximal number of cubes in a building represented by the given pair of drawings.
Examples
|
№ |
stdin |
stdout |
|
1 |
2 4 2 0 3 1 1 1 2 3 1 1 1 |
Minimalni budova obsahuje 7 kostek, maximalni 17 kostek. |
| Ավելացրեց. | Հրանտ Հովհաննիսյան |
| Ամսաթիվ. | 2014-10-08 |
| Ժամանակի սահմանափակումը. | 1s |
| Ծրագրի տեքստի սահմանափակումը. | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Լեզուներ. | Բոլորը բացի ASM32 ASM64 GAWK CLPS CLOJURE D ERL FSHARP FORTRAN GOSU HASK ICON ICK NEM NIM OBJC-CLANG PICO PIKE PYPY PYPY3 PY_NBC RUST SCM guile CHICKEN SED TCL WHITESPACE |
| Աղբյուրը. | CTU Open 2014.C |

 RSS
RSS