| Ուղարկել | Բոլոր լուծումները | Լավագույն լուծումները | Վերադառնալ ցուցակին |
ACM_0149 - INVARIANT POLYNOMIALS |
Consider a real polynomial P (x, y) in two variables. It is called invariant with respect to the rotation by an angle α if
P(x cosα − y sinα , x sinα + y cosα ) = P(x, y)
for all real x and y.
Let’s consider the real vector space formed by all polynomials in two variables of degree not greater than d invariant with respect to the rotation by 2π/n. Your task is to calculate the dimension of this vector space.
You might find useful the following remark: Any polynomial of degree not greater than d can be uniquely written in form
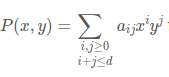
for some real coefficients aij .
Input
The input file contains two positive integers d and n separated by one space. It is guaranteed that they are less than one thousand.
Output
Output a single integer M which is the dimension of the vector space described.
Examples
|
№ |
stdin |
stdout |
|
1 |
1 1 |
3 |
|
2 |
2 2 |
4 |
| Ավելացրեց. | Հրանտ Հովհաննիսյան |
| Ամսաթիվ. | 2014-04-09 |
| Ժամանակի սահմանափակումը. | 1s |
| Ծրագրի տեքստի սահմանափակումը. | 50000B |
| Memory limit: | 1536MB |
| Cluster: | Cube (Intel G860) |
| Լեզուներ. | Բոլորը բացի ASM32 ASM64 GAWK CLPS CLOJURE D ERL FSHARP FORTRAN GOSU HASK ICON ICK NEM NIM OBJC-CLANG PICO PIKE PYPY PYPY3 PY_NBC RUST SCM guile CHICKEN SED TCL WHITESPACE |
| Աղբյուրը. | Northern QF 2003.I |

 RSS
RSS